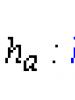Determining the area of a triangle. How can you find the area of a triangle
The triangle is a figure familiar to everyone. And this despite the rich variety of its forms. Rectangular, equilateral, acute, isosceles, obtuse. Each of them is different in some way. But for anyone you need to find out the area of a triangle.
Formulas common to all triangles that use the lengths of sides or heights
The designations adopted in them: sides - a, b, c; heights on the corresponding sides on a, n in, n with.
1. The area of a triangle is calculated as the product of ½, a side and the height subtracted from it. S = ½ * a * n a. The formulas for the other two sides should be written similarly.
2. Heron's formula, in which the semi-perimeter appears (it is usually denoted by the small letter p, in contrast to the full perimeter). The semi-perimeter must be calculated as follows: add up all the sides and divide them by 2. The formula for the semi-perimeter is: p = (a+b+c) / 2. Then the equality for the area of the figure looks like this: S = √ (p * (p - a) * ( р - в) * (р - с)).
3. If you don’t want to use a semi-perimeter, then a formula that contains only the lengths of the sides will be useful: S = ¼ * √ ((a + b + c) * (b + c - a) * (a + c - c) * (a + b - c)). It is slightly longer than the previous one, but it will help out if you have forgotten how to find the semi-perimeter.
General formulas involving the angles of a triangle
Notations required to read the formulas: α, β, γ - angles. They lie opposite sides a, b, c, respectively.
1. According to it, half the product of two sides and the sine of the angle between them is equal to the area of the triangle. That is: S = ½ a * b * sin γ. The formulas for the other two cases should be written in a similar way.
2. The area of a triangle can be calculated from one side and three known angles. S = (a 2 * sin β * sin γ) / (2 sin α).
3. There is also a formula with one known side and two adjacent angles. It looks like this: S = c 2 / (2 (ctg α + ctg β)).
The last two formulas are not the simplest. It's quite difficult to remember them.

General formulas for situations where the radii of inscribed or circumscribed circles are known
Additional designations: r, R - radii. The first is used for the radius of the inscribed circle. The second is for the one described.
1. The first formula by which the area of a triangle is calculated is related to the semi-perimeter. S = r * r. Another way to write it is: S = ½ r * (a + b + c).
2. In the second case, you will need to multiply all the sides of the triangle and divide them by quadruple the radius of the circumscribed circle. In literal expression it looks like this: S = (a * b * c) / (4R).
3. The third situation allows you to do without knowing the sides, but you will need the values of all three angles. S = 2 R 2 * sin α * sin β * sin γ.

Special case: right triangle
This is the simplest situation, since only the length of both legs is required. They are designated by the Latin letters a and b. The area of a right triangle is equal to half the area of the rectangle added to it.
Mathematically it looks like this: S = ½ a * b. It is the easiest to remember. Because it looks like the formula for the area of a rectangle, only a fraction appears, indicating half.
Special case: isosceles triangle
Since it has two equal sides, some formulas for its area look somewhat simplified. For example, Heron's formula, which calculates the area of an isosceles triangle, takes the following form:
S = ½ in √((a + ½ in)*(a - ½ in)).

If you transform it, it will become shorter. In this case, Heron’s formula for an isosceles triangle is written as follows:
S = ¼ in √(4 * a 2 - b 2).
The area formula looks somewhat simpler than for an arbitrary triangle if the sides and the angle between them are known. S = ½ a 2 * sin β.
Special case: equilateral triangle
Usually in problems the side about it is known or it can be found out in some way. Then the formula for finding the area of such a triangle is as follows:
S = (a 2 √3) / 4.

Problems to find the area if the triangle is depicted on checkered paper
The simplest situation is when a right triangle is drawn so that its legs coincide with the lines of the paper. Then you just need to count the number of cells that fit into the legs. Then multiply them and divide by two.
When the triangle is acute or obtuse, it needs to be drawn to a rectangle. Then the resulting figure will have 3 triangles. One is the one given in the problem. And the other two are auxiliary and rectangular. The areas of the last two need to be determined using the method described above. Then calculate the area of the rectangle and subtract from it those calculated for the auxiliary ones. The area of the triangle is determined.
The situation in which none of the sides of the triangle coincides with the lines of the paper turns out to be much more complicated. Then it needs to be inscribed in a rectangle so that the vertices of the original figure lie on its sides. In this case, there will be three auxiliary right triangles.

Example of a problem using Heron's formula
Condition. Some triangle has known sides. They are equal to 3, 5 and 6 cm. You need to find out its area.
Now you can calculate the area of the triangle using the above formula. Under the square root is the product of four numbers: 7, 4, 2 and 1. That is, the area is √(4 * 14) = 2 √(14).
If greater accuracy is not required, then you can take the square root of 14. It is equal to 3.74. Then the area will be 7.48.
Answer. S = 2 √14 cm 2 or 7.48 cm 2.
Example problem with right triangle
Condition. One leg of a right triangle is 31 cm larger than the second. You need to find out their lengths if the area of the triangle is 180 cm 2.
Solution. We will have to solve a system of two equations. The first is related to area. The second is with the ratio of the legs, which is given in the problem.
180 = ½ a * b;
a = b + 31.
First, the value of “a” must be substituted into the first equation. It turns out: 180 = ½ (in + 31) * in. It has only one unknown quantity, so it is easy to solve. After opening the parentheses, the quadratic equation is obtained: 2 + 31 360 = 0. This gives two values for "in": 9 and - 40. The second number is not suitable as an answer, since the length of the side of a triangle cannot be a negative value.
It remains to calculate the second leg: add 31 to the resulting number. It turns out 40. These are the quantities sought in the problem.
Answer. The legs of the triangle are 9 and 40 cm.
Problem of finding a side through the area, side and angle of a triangle
Condition. The area of a certain triangle is 60 cm 2. It is necessary to calculate one of its sides if the second side is 15 cm and the angle between them is 30º.
Solution. Based on the accepted notation, the desired side is “a”, the known side is “b”, the given angle is “γ”. Then the area formula can be rewritten as follows:
60 = ½ a * 15 * sin 30º. Here the sine of 30 degrees is 0.5.
After transformations, “a” turns out to be equal to 60 / (0.5 * 0.5 * 15). That is 16.
Answer. The required side is 16 cm.
Problem about a square inscribed in a right triangle
Condition. The vertex of a square with a side of 24 cm coincides with the right angle of the triangle. The other two lie on the sides. The third belongs to the hypotenuse. The length of one of the legs is 42 cm. What is the area of the right triangle?
Solution. Consider two right triangles. The first one is the one specified in the task. The second one is based on the known leg of the original triangle. They are similar because they have a common angle and are formed by parallel lines.
Then the ratios of their legs are equal. The legs of the smaller triangle are equal to 24 cm (side of the square) and 18 cm (given leg 42 cm subtract the side of the square 24 cm). The corresponding legs of a large triangle are 42 cm and x cm. It is this “x” that is needed in order to calculate the area of the triangle.
18/42 = 24/x, that is, x = 24 * 42 / 18 = 56 (cm).
Then the area is equal to the product of 56 and 42 divided by two, that is, 1176 cm 2.
Answer. The required area is 1176 cm 2.
A triangle is one of the most common geometric shapes, which we become familiar with in elementary school. Every student faces the question of how to find the area of a triangle in geometry lessons. So, what features of finding the area of a given figure can be identified? In this article we will look at the basic formulas necessary to complete such a task, and also analyze the types of triangles.
Types of triangles
You can find the area of a triangle in completely different ways, because in geometry there is more than one type of figure containing three angles. These types include:
- Obtuse.
- Equilateral (correct).
- Right triangle.
- Isosceles.
Let's take a closer look at each of the existing types of triangles.

This geometric figure is considered the most common when solving geometric problems. When the need arises to draw an arbitrary triangle, this option comes to the rescue.
In an acute triangle, as the name suggests, all the angles are acute and add up to 180°.

This type of triangle is also very common, but is somewhat less common than an acute triangle. For example, when solving triangles (that is, several of its sides and angles are known and you need to find the remaining elements), sometimes you need to determine whether the angle is obtuse or not. Cosine is a negative number.
B, the value of one of the angles exceeds 90°, so the remaining two angles can take small values (for example, 15° or even 3°).
To find the area of a triangle of this type, you need to know some nuances, which we will talk about later.
Regular and isosceles triangles

A regular polygon is a figure that includes n angles and whose sides and angles are all equal. This is what a regular triangle is. Since the sum of all the angles of a triangle is 180°, then each of the three angles is 60°.
A regular triangle, due to its property, is also called an equilateral figure.
It is also worth noting that only one circle can be inscribed in a regular triangle, and only one circle can be described around it, and their centers are located at the same point.

In addition to the equilateral type, one can also distinguish an isosceles triangle, which is slightly different from it. In such a triangle, two sides and two angles are equal to each other, and the third side (to which equal angles are adjacent) is the base.
The figure shows an isosceles triangle DEF whose angles D and F are equal and DF is the base.
Right triangle

A right triangle is so named because one of its angles is right, that is, equal to 90°. The other two angles add up to 90°.
The largest side of such a triangle, lying opposite the 90° angle, is the hypotenuse, while the remaining two sides are the legs. For this type of triangle, the Pythagorean theorem applies:
The sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
The figure shows a right triangle BAC with hypotenuse AC and legs AB and BC.
To find the area of a triangle with a right angle, you need to know the numerical values of its legs.
Let's move on to the formulas for finding the area of a given figure.
Basic formulas for finding area
In geometry, there are two formulas that are suitable for finding the area of most types of triangles, namely for acute, obtuse, regular and isosceles triangles. Let's look at each of them.
By side and height
This formula is universal for finding the area of the figure we are considering. To do this, it is enough to know the length of the side and the length of the height drawn to it. The formula itself (half the product of the base and the height) is as follows:
where A is the side of a given triangle, and H is the height of the triangle.

For example, to find the area of an acute triangle ACB, you need to multiply its side AB by the height CD and divide the resulting value by two.
However, it is not always easy to find the area of a triangle this way. For example, to use this formula for an obtuse triangle, you need to extend one of its sides and only then draw an altitude to it.
In practice, this formula is used more often than others.
On both sides and corner
This formula, like the previous one, is suitable for most triangles and in its meaning is a consequence of the formula for finding the area by side and height of a triangle. That is, the formula in question can be easily derived from the previous one. Its formulation looks like this:
S = ½*sinO*A*B,
where A and B are the sides of the triangle, and O is the angle between sides A and B.
Let us recall that the sine of an angle can be viewed in a special table named after the outstanding Soviet mathematician V. M. Bradis.
Now let's move on to other formulas that are suitable only for exceptional types of triangles.
Area of a right triangle
In addition to the universal formula, which includes the need to find the altitude in a triangle, the area of a triangle containing a right angle can be found from its legs.
Thus, the area of a triangle containing a right angle is half the product of its legs, or:
where a and b are the legs of a right triangle.
Regular triangle
This type of geometric figure is different in that its area can be found with the indicated value of only one of its sides (since all sides of a regular triangle are equal). So, when faced with the task of “finding the area of a triangle when the sides are equal,” you need to use the following formula:
S = A 2 *√3 / 4,
where A is the side of the equilateral triangle.
Heron's formula
The last option for finding the area of a triangle is Heron's formula. In order to use it, you need to know the lengths of the three sides of the figure. Heron's formula looks like this:
S = √p·(p - a)·(p - b)·(p - c),
where a, b and c are the sides of a given triangle.
Sometimes the problem is given: “the area of a regular triangle is to find the length of its side.” In this case, we need to use the formula we already know for finding the area of a regular triangle and derive from it the value of the side (or its square):
A 2 = 4S / √3.
Examination tasks
There are many formulas in GIA problems in mathematics. In addition, quite often it is necessary to find the area of a triangle on checkered paper.
In this case, it is most convenient to draw the height to one of the sides of the figure, determine its length from the cells and use the universal formula for finding the area:
So, after studying the formulas presented in the article, you will not have any problems finding the area of a triangle of any kind.
As you may remember from your school geometry curriculum, a triangle is a figure formed from three segments connected by three points that do not lie on the same straight line. A triangle forms three angles, hence the name of the figure. The definition may be different. A triangle can also be called a polygon with three angles, the answer will also be correct. Triangles are divided according to the number of equal sides and the size of the angles in the figures. Thus, triangles are distinguished as isosceles, equilateral and scalene, as well as rectangular, acute and obtuse, respectively.
There are a lot of formulas for calculating the area of a triangle. Choose how to find the area of a triangle, i.e. Which formula to use is up to you. But it is worth noting only some of the notations that are used in many formulas for calculating the area of a triangle. So, remember:
S is the area of the triangle,
a, b, c are the sides of the triangle,
h is the height of the triangle,
R is the radius of the circumscribed circle,
p is the semi-perimeter.
Here are the basic notations that may be useful to you if you completely forgot your geometry course. Below are the most understandable and uncomplicated options for calculating the unknown and mysterious area of a triangle. It is not difficult and will be useful both for your household needs and for helping your children. Let's remember how to calculate the area of a triangle as easily as possible:
In our case, the area of the triangle is: S = ½ * 2.2 cm * 2.5 cm = 2.75 sq. cm. Remember that area is measured in square centimeters (sqcm).
Right triangle and its area.
A right triangle is a triangle in which one angle is equal to 90 degrees (hence called right). A right angle is formed by two perpendicular lines (in the case of a triangle, two perpendicular segments). In a right triangle there can only be one right angle, because... the sum of all angles of any one triangle is equal to 180 degrees. It turns out that 2 other angles should divide the remaining 90 degrees, for example 70 and 20, 45 and 45, etc. So, you remember the main thing, all that remains is to find out how to find the area of a right triangle. Let's imagine that we have such a right triangle in front of us, and we need to find its area S.

1. The simplest way to determine the area of a right triangle is calculated using the following formula:

In our case, the area of the right triangle is: S = 2.5 cm * 3 cm / 2 = 3.75 sq. cm.
In principle, there is no longer any need to verify the area of the triangle in other ways, because Only this one will be useful and will help in everyday life. But there are also options for measuring the area of a triangle through acute angles.
2. For other calculation methods, you must have a table of cosines, sines and tangents. Judge for yourself, here are some options for calculating the area of a right triangle that can still be used:

We decided to use the first formula and with some minor blots (we drew it in a notebook and used an old ruler and protractor), but we got the correct calculation:
S = (2.5*2.5)/(2*0.9)=(3*3)/(2*1.2). We got the following results: 3.6=3.7, but taking into account the shift of cells, we can forgive this nuance.
Isosceles triangle and its area.
If you are faced with the task of calculating the formula for an isosceles triangle, then the easiest way is to use the main and what is considered to be the classical formula for the area of a triangle.

But first, before finding the area of an isosceles triangle, let’s find out what kind of figure it is. An isosceles triangle is a triangle in which two sides have the same length. These two sides are called lateral, the third side is called the base. Do not confuse an isosceles triangle with an equilateral triangle, i.e. a regular triangle with all three sides equal. In such a triangle there are no special tendencies to the angles, or rather to their size. However, the angles at the base in an isosceles triangle are equal, but different from the angle between equal sides. So, you already know the first and main formula; it remains to find out what other formulas for determining the area of an isosceles triangle are known.
Concept of area
The concept of the area of any geometric figure, in particular a triangle, will be associated with a figure such as a square. For the unit area of any geometric figure we will take the area of a square whose side is equal to one. For completeness, let us recall two basic properties for the concept of areas of geometric figures.
Property 1: If geometric figures are equal, then their areas are also equal.
Property 2: Any figure can be divided into several figures. Moreover, the area of the original figure is equal to the sum of the areas of all its constituent figures.
Let's look at an example.
Example 1
Obviously, one of the sides of the triangle is a diagonal of a rectangle, one side of which has a length of $5$ (since there are $5$ cells), and the other is $6$ (since there are $6$ cells). Therefore, the area of this triangle will be equal to half of such a rectangle. The area of the rectangle is
Then the area of the triangle is equal to
Answer: $15$.
Next, we will consider several methods for finding the areas of triangles, namely using the height and base, using Heron’s formula and the area of an equilateral triangle.
How to find the area of a triangle using its height and base
Theorem 1
The area of a triangle can be found as half the product of the length of a side and the height to that side.
Mathematically it looks like this
$S=\frac(1)(2)αh$
where $a$ is the length of the side, $h$ is the height drawn to it.
Proof.
Consider a triangle $ABC$ in which $AC=α$. The height $BH$ is drawn to this side, which is equal to $h$. Let's build it up to the square $AXYC$ as in Figure 2.

The area of rectangle $AXBH$ is $h\cdot AH$, and the area of rectangle $HBYC$ is $h\cdot HC$. Then
$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$
Therefore, the required area of the triangle, by property 2, is equal to
$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$
The theorem has been proven.
Example 2
Find the area of the triangle in the figure below if the cell has an area equal to one
The base of this triangle is equal to $9$ (since $9$ is $9$ squares). The height is also $9$. Then, by Theorem 1, we get
$S=\frac(1)(2)\cdot 9\cdot 9=40.5$
Answer: $40.5$.
Heron's formula
Theorem 2
If we are given three sides of a triangle $α$, $β$ and $γ$, then its area can be found as follows
$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
here $ρ$ means the semi-perimeter of this triangle.
Proof.
Consider the following figure:
By the Pythagorean theorem, from the triangle $ABH$ we obtain
From the triangle $CBH$, according to the Pythagorean theorem, we have
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βx-x^2$
From these two relations we obtain the equality
$γ^2-x^2=α^2-β^2+2βx-x^2$
$x=\frac(γ^2-α^2+β^2)(2β)$
$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$
$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$
$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$
Since $ρ=\frac(α+β+γ)(2)$, then $α+β+γ=2ρ$, which means
$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$
$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$
$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$
$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
By Theorem 1, we get
$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
Concept of area
The concept of the area of any geometric figure, in particular a triangle, will be associated with a figure such as a square. For the unit area of any geometric figure we will take the area of a square whose side is equal to one. For completeness, let us recall two basic properties for the concept of areas of geometric figures.
Property 1: If geometric figures are equal, then their areas are also equal.
Property 2: Any figure can be divided into several figures. Moreover, the area of the original figure is equal to the sum of the areas of all its constituent figures.
Let's look at an example.
Example 1
Obviously, one of the sides of the triangle is a diagonal of a rectangle, one side of which has a length of $5$ (since there are $5$ cells), and the other is $6$ (since there are $6$ cells). Therefore, the area of this triangle will be equal to half of such a rectangle. The area of the rectangle is
Then the area of the triangle is equal to
Answer: $15$.
Next, we will consider several methods for finding the areas of triangles, namely using the height and base, using Heron’s formula and the area of an equilateral triangle.
How to find the area of a triangle using its height and base
Theorem 1
The area of a triangle can be found as half the product of the length of a side and the height to that side.
Mathematically it looks like this
$S=\frac(1)(2)αh$
where $a$ is the length of the side, $h$ is the height drawn to it.
Proof.
Consider a triangle $ABC$ in which $AC=α$. The height $BH$ is drawn to this side, which is equal to $h$. Let's build it up to the square $AXYC$ as in Figure 2.

The area of rectangle $AXBH$ is $h\cdot AH$, and the area of rectangle $HBYC$ is $h\cdot HC$. Then
$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$
Therefore, the required area of the triangle, by property 2, is equal to
$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$
The theorem has been proven.
Example 2
Find the area of the triangle in the figure below if the cell has an area equal to one
The base of this triangle is equal to $9$ (since $9$ is $9$ squares). The height is also $9$. Then, by Theorem 1, we get
$S=\frac(1)(2)\cdot 9\cdot 9=40.5$
Answer: $40.5$.
Heron's formula
Theorem 2
If we are given three sides of a triangle $α$, $β$ and $γ$, then its area can be found as follows
$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
here $ρ$ means the semi-perimeter of this triangle.
Proof.
Consider the following figure:
By the Pythagorean theorem, from the triangle $ABH$ we obtain
From the triangle $CBH$, according to the Pythagorean theorem, we have
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βx-x^2$
From these two relations we obtain the equality
$γ^2-x^2=α^2-β^2+2βx-x^2$
$x=\frac(γ^2-α^2+β^2)(2β)$
$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$
$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$
$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$
Since $ρ=\frac(α+β+γ)(2)$, then $α+β+γ=2ρ$, which means
$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$
$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$
$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$
$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$
By Theorem 1, we get
$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$